
Monitoring chemical reactions (chemistry only)
C5: Monitoring and controlling chemical reactions
Percentage Yield
A perfect reaction will 100% convert reactant into product. When we work out how much product we’ve made, compared to what we expect, it isn’t always 100% … for a few reasons:
- incomplete reactions (left over reactants)
- practical losses during the experiment (product still left on equipment)
- competing, unwanted reactions (side reactions)
We can work out a % of what we have made, compared to what we expected:
% yield = (actual yield ÷ theoretical yield) x 100
If a reaction should produce 50 g of product, but only produces 42 g, then we can use the above equation to calculate that the percentage yield is 84% ((42 ÷ 50) x 100)

Atom Economy
Atom economy is a measure of how many of the atoms from the starting material end up in the desired product.
Many reactions make more than one chemical, but often we only really want one of them. We can use this calculation to work out how ‘green’ our reaction is:
% atom economy = (RFM of product ÷ RFM of all reactants) x 100
If we have a high atom economy, then the majority of the atoms we put into the equation are what we get out!
A reaction that only produces one product, will have a 100% atom economy.

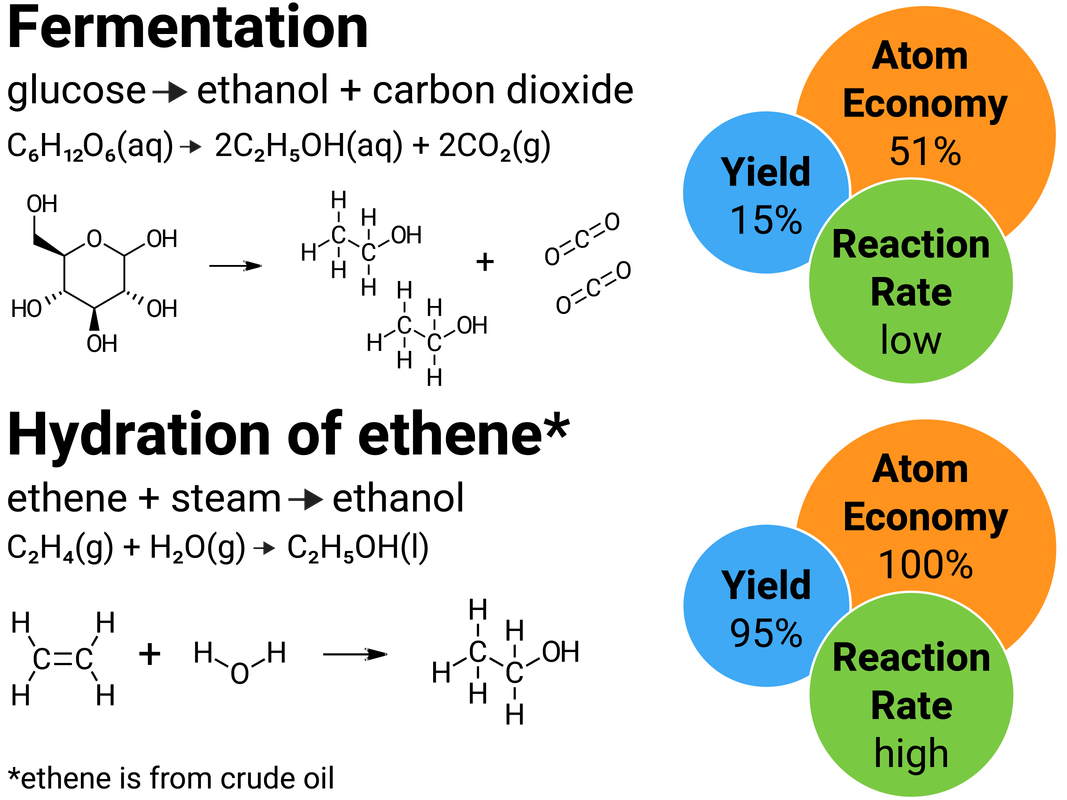
Reaction Pathways
Higher Tier
Usually, there is more than one way to make a particular chemical. A reaction pathway describes the sequence of reactions needed to produce the desired product.
The pathway chosen for a product depends on factors such as:
- percentage yield
- atom economy
- rate of reaction
- equilibrium position
- usefulness of by-products
Concentration
A solution is formed when a solute dissolves in a solvent. The concentration of a solution is a measure of the mass, or amount of solute, dissolved in a given volume of solvent. The more concentrated
the solution, the more particles it contains in a given volume.
Higher Tier
The concentration of a solution can be calculated using:
- the moles of dissolved solute (in mol)
- the volume of solvent (in dm3)
concentration = moles of solute ÷ volume of solvent
The units for concentration are mol/dm3, but they may also be written as moldm-3 - don't worry as these mean the same thing.
Converting from grams to moles
You need to be able to calculate concentration in gdm-3 and be able to convert these units into mol/dm3.
To do this, think back to our moles equations, where:
moles = mass ÷ Mr
For example, a solution of sodium hydroxide has the concentration of 5 g/dm3.
To convert it into mol/dm3, we divide 5 ("the mass") by 40 (the Mr of NaOH).
This gives a concentration of 0.125 mol/dm3.

Volume unit conversions
- divide by 1000 to convert from cm3 to dm3
- multiply by 1000 to convert from dm3 to cm3
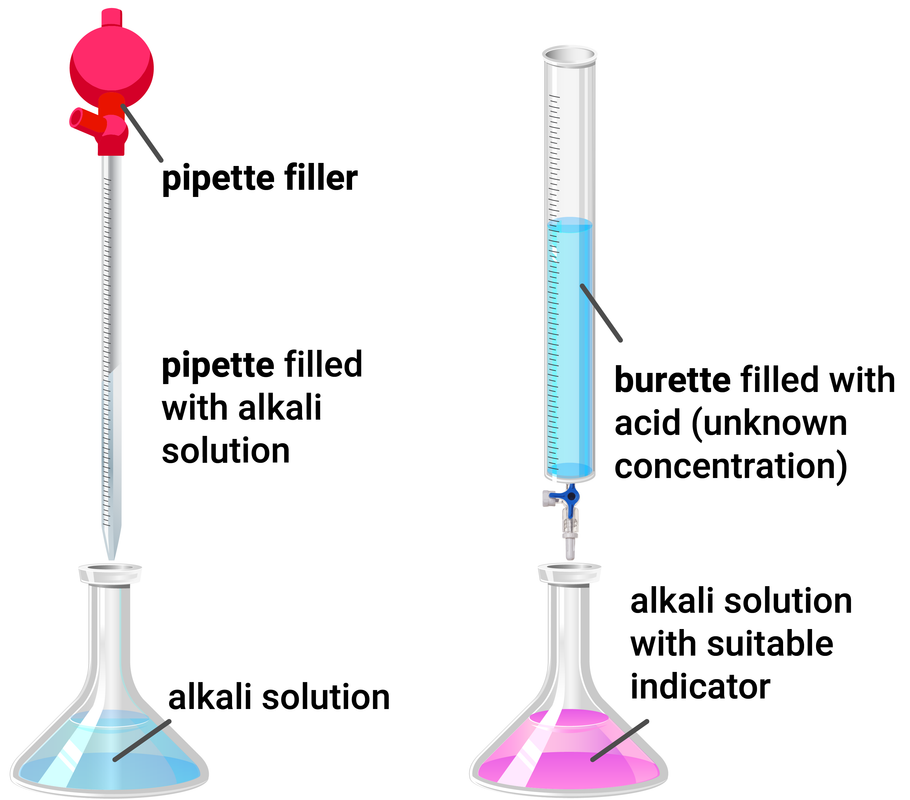
Titration Calculations
Higher Tier
Knowing the concentration of a solution and the volume we can work out the number of moles in a solution using the equation:
concentration = moles of solute ÷ volume of solvent
Worked Example
NaOH + HCl → NaCl + H2O
During a titration, 25 ml of sodium hydroxide was used to neutralise hydrochloric acid. This is the same as 0.025 dm3.
If the concentration of the alkali is 0.12 mol/dm3, then the amount of moles used is 0.025 x 0.12 = 0.003 moles.
| NaOH | HCl | |
|---|---|---|
| concentration | 0.12 | ? |
| volume | 0.025 | ? |
| moles | 0.003 | ? |
If hydrochloric acid (unknown concentration) completely neutralises the alkali then we know that 0.003 moles of acid were also present (because the balanced symbol equation shows a 1:1 ratio of acid reacting with alkali).
If 26.8 ml of acid were needed to neutralise 25 ml of alkali, we know 0.0268 dm3 acid were used.
| NaOH | HCl | |
|---|---|---|
| concentration | 0.12 | ? |
| volume | 0.025 | 0.0268 |
| moles | 0.003 | 0.003 |
The concentration of the acid then uses the above equation again (but rearranged):
concentration = moles ÷ volume
So the concentration of the acid used = 0.003 ÷ 0.0268 = 0.11 mol/dm3
| rough | run 1 | run 2 | run 3 | |
|---|---|---|---|---|
| final reading | 15.05 | 14.70 | 14.75 | 14.70 |
| initial reading | 0.05 | 0.05 | 0.00 | 0.00 |
| titre (ml) | 15.00 | 14.65 | 14.75 | 14.70 |
Calculating average titres
When completing a titration, you will have multiple readings which you need to calculate an average reading for.
It is important that the titres you include in your calculation are concordant (within 0.10 ml). If they are not, you will lose marks in an exam.
Above are some results from a titration experiment.
The average titre for these results would only include the values from run 1, 2 and 3 as these are the only concordant results.
Avagadro's Law
Higher Tier
Avogadro's law states that equal volumes of different gases contain an equal number of molecules (this only applies at room temperature and pressure).
The molar volume is the volume occupied by one mole of molecules of any gas at room temperature and pressure.
(The molar volume will be provided as 24 dm3 or 24000 cm3 in calculations where it is required)
Avogadro's law can be used to calculate the volumes of gases involved in reactions:
hydrogen reacts with chlorine to form hydrogen chloride
H2(g) + Cl2(g) → 2HCl(g)
The mole ratio of hydrogen to chlorine is 1:1, and of reactants to products is 1:2. This means, for example:
- 1 cm3 of hydrogen reacts exactly with 1 cm3 of chlorine, and will make 2 cm3 of hydrogen chloride
- 250 cm3 of hydrogen reacts exactly with 250 cm3 of chlorine, and will make 500 cm3 of hydrogen chloride
- 1 dm3 of hydrogen reacts exactly with 1 dm3 of chlorine, and will make 2 dm3 of hydrogen chloride
Calculations with Gases
Higher Tier
2Na(s) + 2H2O(l) → 2NaOH(aq) + H2(g)
5.0 g of sodium reacts fully with water. Calculate the volume of hydrogen produced.
(Ar of Na = 23, molar volume = 24 dm3)
| Na | H2 | |
|---|---|---|
| mass/volume | 5.0 g | ? |
| Mr | 23 | x |
| moles | 0.217 | ? |
If sodium completely reacts with water, then we know that 0.217 moles of sodium will make 0.109 moles of hydrogen (because the balanced symbol equation shows a 2:1 ratio of sodium reacting to make hydrogen).
| Na | H2 | |
|---|---|---|
| mass/volume | 5.0 g | ? |
| Mr | 23 | x |
| moles | 0.217 | 0.109 |
1 mole of gas takes up a volume of 24 dm3
So the volume of hydrogen produced = 0.109 x 24 = 2.61 dm3
