Calculations Involving Masses

Key Concepts in Chemistry

More in this topic
Links

RAM and RFM

Relative Atomic Mass  (RAM or Ar)

An atom’s mass number is the sum of its protons and neutrons. Carbon has 6 neutrons and 6 protons so we say it has a mass of 12. You can find this information on a Periodic Table.

However, relative atomic mass takes into account that some elements have isotopes. These are atoms of the same element, but with different numbers of neutrons. The Periodic Table contains a list of every element, with their relative atomic masses.

We can take an average of all an element's isotope mass numbers to work out the relative atomic mass of that element for ourselves (see diagram - higher tier only).

Relative Formula Mass  (RFM or Mr )

This is like relative atomic mass, but we are working out the mass of a compound. You have to add all of the relative atomic masses of each atom, or ion, together to calculate an RFM, for example water (H₂O):

  • there are two hydrogen atoms, each with an atomic mass of 1... so 1 × 2 = 2
  • there is one oxygen atom, which has an atomic mass of 16
  • in total the relative formula mass of water is 16 + 2 = 18

Higher Tier

Calculating the relative atomic mass from isotope masses and abundancies is higher tier only.

Relative Atomic Mass

Empirical Formula

An empirical formula is the simplest whole number ratio of atoms in a substance. 

Substances that are made of simple molecules also have a molecular formula. This represents the actual number of atoms of each element in one molecule.

Ethene has the molecular formula C2H4, but the empirical formula CH2. Sometimes the empirical formula is the same as the molecular formula (e.g. water has the formula H2O, this cannot be simplified any further).

You can calculate the formulae of simple compounds from reacting masses or percentage composition. These formula are called empirical formulae. 

Empirical Formula Calculations

Experimental evidence

It's possible to complete a practical to work out the empirical formula of a substance. For example, calculating the empirical formula of magnesium oxide, by reacting magnesium with oxygen in the air:

  • record the mass of a crucible with, and without magnesium 
  • complete the reaction, then record the mass of crucible with product (magnesium oxide)
  • calculate the mass of oxygen used
  • using the mass of magnesium and oxygen used to make magnesium oxide, we can work out its empirical formula (see below)
action Mg O
write the masses
 0.3 g 0.2 g
Write the Ar values
 24 16
Divide masses by Ar
 0.1 ÷ 24 = 0.125 0.2 ÷ 16 = 0.125
Divide by the smallest number
 0.0125 ÷ 0.0125 = 1 0.0125 ÷ 0.0125 = 1

This shows that magnesium and oxygen are in a 1:1 ratio, so the empirical formula is MgO (for every 1 Mg, there is 1 O).

Worked Example 1

Calculate the empirical formula of calcium chloride, when 10.0 g of calcium reacts with 17.8 g of chlorine.
(RAM: Ca=40, and Cl=35.5)

  • Divide the mass of each element by its relative atomic mass
  • Ca = 10.0 ÷ 40 = 0.25
  • Cl = 17.8 ÷ 35.5 = 0.5
  • Divide the answers by the smallest number to find the simplest ratio
  • Ca = 0.25 ÷ 0.25 = 1
  • Cl = 0.5 ÷ 0.25 = 2
  • The empirical formula then is CaCl2
    •

    Worked Example 2

    The empirical formula for glucose is CH2O and its relative formula mass is 180. Determine the molecular formula for glucose.
    (RAM: C=12, O=16, and H=1)

  • Find the empirical formula mass = C (12) + H (2×1) + O (16) = 30
  • Divide the RFM by the empirical formula mass = 180 ÷ 30 = 6
  • The molecular formula is 6 times the empirical formula, so the molecular formula is C6H12O6
    •

    Conservation of Mass

    The law of conservation of mass states that no atoms are created or destroyed during a chemical reaction, they are only rearranged. This means that the mass of the products must be the same as the mass of the reactants.

    Closed systems

    No substances can enter or exit a closed system. A simple closed system in the lab could just be a sealed flask. Sometimes reactions that happen in open beakers are still closed systems (because nothing enters or exits the system). These include:

    • acid-alkali neutralisation reactions, which produce salt solutions
    • precipitation reactions, which produce an insoluble precipitate (solid)

    Non-enclosed systems

    Substances can enter or exit a non-enclosed system. These systems are often open flasks, or crucibles, that let gases enter or exit.

    If a gas escapes, it can look like the total mass has decreased. If a gas is added, the total mass will look as if it has increased. However, the total mass stays the same if the mass of the gas is included in calculations.

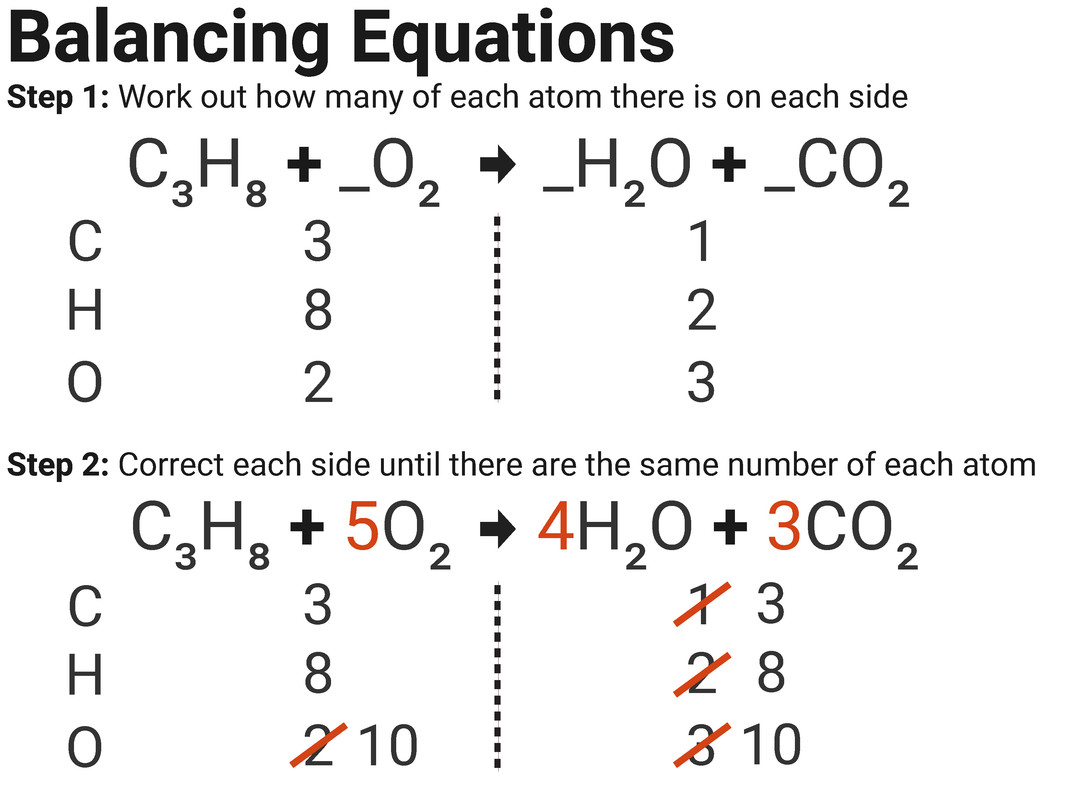
    Balancing Equations

    Worked Example 1

    In a reaction between propane and oxygen, 36 g of water is produced. Use the balanced symbol equation below to calculate the mass of propane needed for this reaction (assume oxygen is in excess).
    (RAM: C=12, H=1, and O=16)

    C3H8 + 5O2 → 4H2O + 3CO2

  • Look at the ratio of substances in the equation
    1C3H8 is needed for every 4H2O
  • Divide the known substance's mass (H2O) by its RFM
    = 36 ÷ (16 + (2×1)) = 2
  • You only have 2H2O, not 4, so using the ratio of 1:4 you now know you only have 0.5 (1 ÷ 2) C3H8
  • Multiply the known number of C3H8 particles by its RFM
    = 0.5 × ((12 × 3) + (1×8)) = 22
  • So 22 g of propane are needed to make 36 g of water

    • Worked Example 2

    In a reaction between propane and oxygen, 10 g of oxygen is used. Use the balanced symbol equation below to calculate the mass of carbon dioxide produced (assume propane is in excess).
    (RAM: C=12, H=1, and O=16)

    C3H8 + 5O2 → 4H2O + 3CO2

  • Look at the ratio of substances in the equation
    5O2 is needed for every 3CO2
  • Divide the known substance's mass (O2) by its RFM
    = 10 ÷ (16 × 2)) = 0.3125
  • You only have 0.3125 O2, not 5, so using the ratio of 5:3 you now know you only have 0.1875 ((0.3125 ÷ 5)× 3) CO2
  • Multiply the known number of CO2 particles by its RFM
    = 0.1875 × (12 + (16×2)) = 8.25
  • So 8.25 g of carbon dioxide are made from 10 g of oxygen

    • Concentration

    A solution is formed when a solute dissolves in a solvent. The concentration of a solution is a measure of the mass, or amount of solute, dissolved in a given volume of solvent. The more concentrated the solution, the more particles it contains in a given volume.

    Calculating concentration

    The concentration of a solution can be calculated using:

    • the mass of dissolved solute (in g)
    • the volume of solvent (in dm3)

    concentration = mass of solute  ÷ volume of solvent

    The units for concentration are g/dm3, but they may also be written as gdm-3 - don't worry as these mean the same thing.

    Volume unit conversions

    Sometimes volumes can be quoted in ml, rather than cm3. These units describe the same volume. For example, 250 ml = 250 cm3.
    If your volume is given in cm3, then you will need to convert it into dm3 before it can be used in this calculation.

    • divide by 1000 to convert from cm3 to dm3
    • multiply by 1000 to convert from dm3 to cm3

    Concentration Calculations

    The Mole

    Higher Tier

    Chemical amounts are measured in moles (symbol: mol). The mass of one mole of substance in grams is equal to the substance’s RAM/RFM. One mole of a substance contains the same number of particles, atoms, molecules or ions as one mole of any other substance.

    The number of atoms, molecules or ions in a mole of a given substance is the Avogadro constant. The value of the Avogadro constant is 6.02×10²³ per mole. This means that for every one mole of substance (no matter the substance), it will always contain 6.02×10²³ particles.

    name of
    element    		 relative
    atomic mass    		 1 mole
    (mass)    		 1 mole
    (particles)
    carbon 12 12 g 6.02×10²³
    sodium 23 23 g 6.02×10²³

    moles = mass (g) ÷ RFM

    We can use this equation to calculate the number of moles of a chemical in a given amount of mass.

    Mole Calculations

    Worked Example 1

    Calculate the number of particles in 20 g of MgO
    (RAM: Mg=24, and O=16)

  • MgO has an RFM of 40
  • we can calculate that there are 0.5 moles of MgO in 20 g by dividing the mass by the RFM (20 ÷ 40)
  • there are 6.02 × 1023 particles in every 1 mole of a substance
  • there are 0.5 moles, so 6.02 × 1023 ÷ 2
    = 3.01 × 1023 particles

    • Worked Example 2

    Calculate the number of moles of oxygen needed to make 6 moles of magnesium oxide. 
    (RAM: Mg=24, and O=16)

    2Mg + O2 → 2MgO

  • For every 1 mole of O2 we make 2 moles of MgO
  • we made 6 moles of MgO so we need 3 moles of O2 (6 ÷ 2)

    • Worked Example 3

    Calculate the number of moles of magnesium oxide created, when 12 g of magnesium is burned in air. 
    (RAM: Mg=24, and O=16)

    2Mg + O2 → 2MgO

  • For every 2 moles of Mg we make 2 moles of MgO
  • we have 0.5 moles of Mg (12 ÷ 24) so we make 0.5 moles of MgO
  • MgO has an RFM of 40...
  • so we make 20 g of MgO (0.5 × 40)

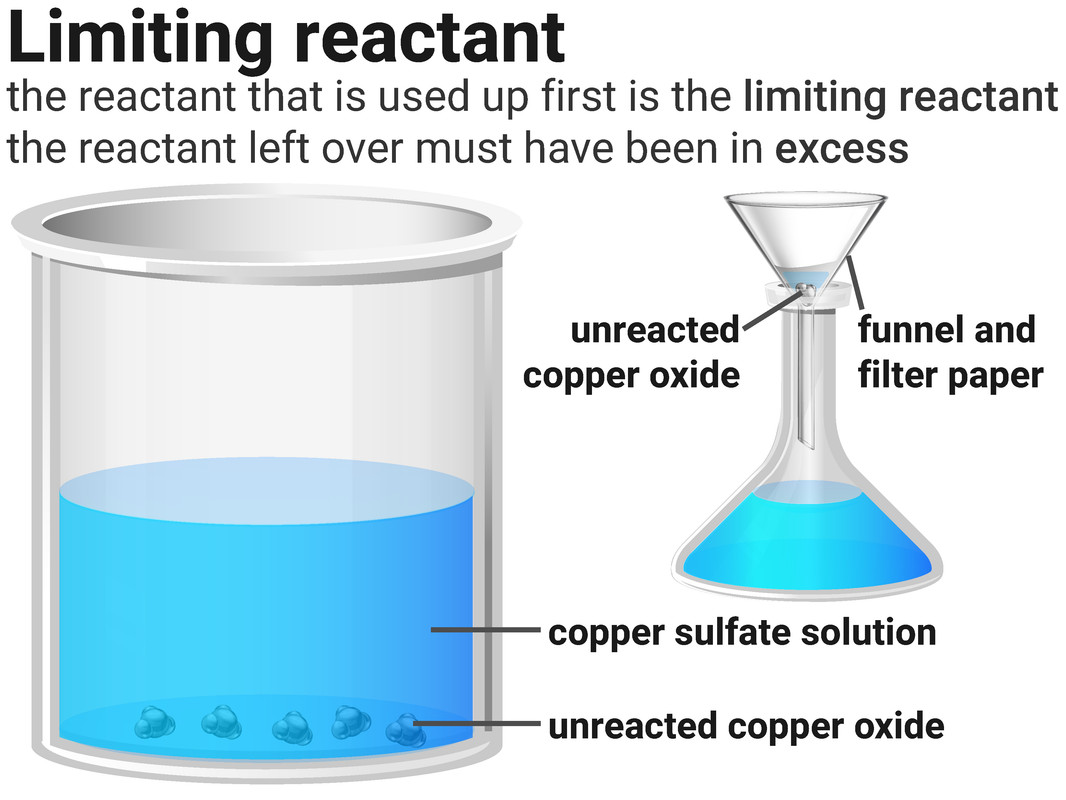
    • Limiting Reactants

    Higher Tier

    Reactions stop when one of the reactants is used up. This is because the other reactant has nothing more to react with, and so some of it will be left over. 

    The substance that runs out is called the limiting reactant. The one left over we say has been added in excess.

    The stoichiometry of a reaction is the ratio of the amounts of each substance in the balanced equation. It can be worked out using masses found by experiment.

    action Mg O2
    calculate amounts
    		 0.6 ÷ 24 = 0.025 mol 0.2 ÷ 16 = 0.0125 mol
    Divide by the smallest number 0.25 ÷ 0.0125 = 2 0.125 ÷ 0.0125 = 1

    This means that 2 moles of Mg reacts with 1 mol of O2, so the left-hand side of the equation is: 2Mg + O2

    Then balancing the equation gives us: 2Mg + O2 → 2MgO

    Limiting reactant